Revisiting the Bethe-Hessian: Improved Community Detection in Sparse Heterogeneous Graphs

Abstract

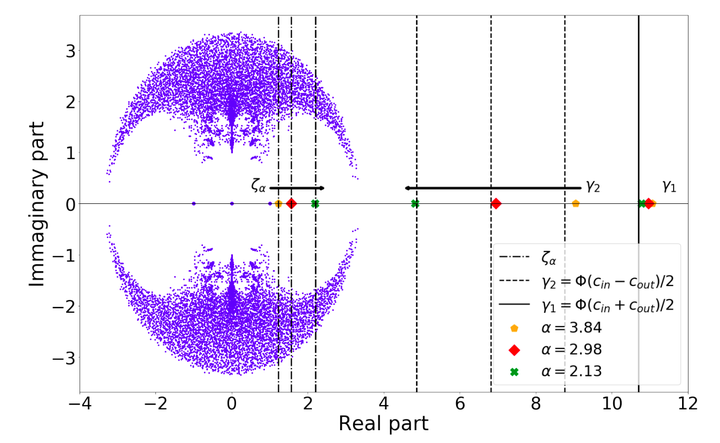
Spectral clustering is one of the most popular, yet still incompletely understood, methods for community detection on graphs. This article studies spectral clustering based on the Bethe-Hessian matrix $H_r = (r^2 − 1)I_n + D − rA$ for sparse heterogeneous graphs (following the degree-corrected stochastic block model) in a two-class setting. For a specific value $r = \zeta$, clustering is shown to be insensitive to the degree heterogeneity. We then study the behavior of the informative eigenvector of $H_{\zeta}$ and, as a result, predict the clustering accuracy. The article concludes with an overview of the generalization to more than two classes along with extensive simulations on synthetic and real networks corroborating our findings.