Learning distributed representations with efficient SoftMax normalization

Abstract

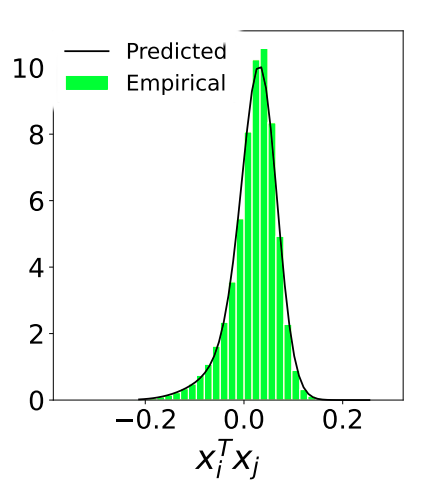
Learning distributed representations, or embeddings, that encode the relational similarity patterns among objects is a relevant task in machine learning. A popular method to learn the embedding matrices $X$, $Y$ is optimizing a loss function of the term ${\rm SoftMax}(XY^T)$. The complexity required to calculate this term, however, runs quadratically with the problem size, making it a computationally heavy solution. In this article, we propose a lineartime heuristic approximation to compute the normalization constants of ${\rm SoftMax}(XY^T)$ for embedding vectors with bounded norms. We show on some pre-trained embedding datasets that the proposed estimation method achieves higher or comparable accuracy with competing methods. From this result, we design an efficient and task-agnostic algorithm that learns the embeddings by optimizing the cross entropy between the softmax and a set of probability distributions given as inputs. The proposed algorithm is interpretable and easily adapted to arbitrary embedding problems. We consider a few use cases and observe similar or higher performances and a lower computational time than similar “2Vec” algorithms.