Nishimori meets Bethe: a spectral method for node classification in sparse weighted graphs

Abstract

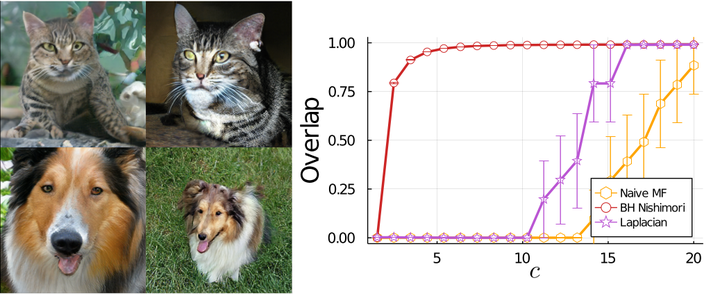
This article unveils a new relation between the Nishimori temperature parametrizing a distribution P and the Bethe free energy on random Erdős-Rényi graphs with edge weights distributed according to P. Estimating the Nishimori temperature being a task of major importance in Bayesian inference problems, as a practical corollary of this new relation, a numerical method is proposed to accurately estimate the Nishimori temperature from the eigenvalues of the Bethe Hessian matrix of the weighted graph. The algorithm, in turn, is used to propose a new spectral method for node classification in weighted (possibly sparse) graphs. The superiority of the method over competing state-of-the-art approaches is demonstrated both through theoretical arguments and real-world data experiments.